Árvores de decisão
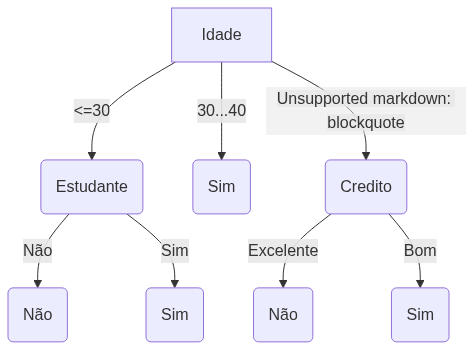
Uma árvore de decisão é um modelo de aprendizado de máquina que utiliza uma estrutura de árvore para tomar decisões com base em condições nos dados de entrada.
Essa estrutura hierárquica consiste em nós que representam testes sobre atributos e arestas que conectam os nós, indicando os resultados desses testes.
Cada nó interno da árvore representa um teste em um atributo específico, enquanto as folhas representam as classes ou valores de saída.
Ao percorrer a árvore da raiz até uma folha, os dados de entrada são avaliados de acordo com os testes em cada nó, seguindo o caminho apropriado até alcançar uma folha, onde é tomada a decisão final.
Principais Algoritmos
ID3 (Iterative Dichotomiser 3)
É um dos primeiros algoritmos de árvore de decisão e utiliza o ganho de informação como critério para selecionar a melhor divisão em cada nó. No entanto, o ID3 não lida diretamente com atributos numéricos.
C4.5
É uma extensão do ID3 e possui melhorias, incluindo a capacidade de lidar com atributos numéricos e valores ausentes. Além disso, o C4.5 utiliza a razão de ganho como métrica de seleção de atributos, em vez do ganho de informação utilizado pelo ID3.
CART (Classification and Regression Trees)
É um algoritmo que pode ser usado tanto para problemas de classificação quanto de regressão. O CART constrói árvores binárias e utiliza o índice de Gini como critério de divisão. Ele busca minimizar a impureza nos nós da árvore.
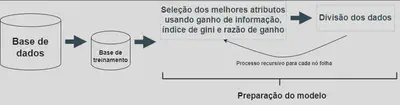
Critérios de divisão
Entropia
A entropia é uma medida de impureza ou desordem nos dados em um algoritmo de árvore de decisão. Ela é utilizada para avaliar o quão homogêneos ou heterogêneos são os exemplos de uma determinada classe em um conjunto de dados.
É calculada a partir da distribuição das classes no conjunto de dados. Quanto maior a entropia, maior a incerteza sobre a classe de um exemplo. Quanto menor a entropia, mais homogêneos são os exemplos em relação à classe.
Cálculo da entropia (E)
$$ \text{E(S)} = \sum_{i=1}^c -p_i\log_2 p_i$$em que `\(p_i\)` é a proporção de exemplos na classe `\(i\)` da amostra de treinamento S.
A entropia mede a “impureza” de S!
No contexto das árvores de decisão a entropia é usada para estimar a aleatoriedade da variável a prever a classe.
Ganho de Informação (G)
O ganho de informação é uma métrica utilizada para medir a relevância de um atributo na divisão dos dados. Ele indica a quantidade de informação que um atributo fornece sobre a classe ou variável de saída.
Cálculo do ganho de informação
$$ \text{G}(S, A) = \text{E}(S) - \text{E}(S,A)$$em que `$$E(S,A) = \sum_{v\in \text{valores de } A} \dfrac{|S_v|}{|S|} \times \text{E}(S_v)$$` é a entropia do atributo A.
Razão de ganho
Também conhecida como gain ratio, é uma métrica utilizada para selecionar os melhores atributos de divisão, levando em consideração o viés por atributos com muitos valores possíveis.
Enquanto o ganho de informação mede a redução da entropia dos dados após a divisão com base em um atributo, a razão de ganho ajusta esse valor, levando em consideração o número de valores distintos do atributo.
Essa correção é importante para evitar que atributos com muitos valores possíveis tenham vantagem sobre atributos com menos valores.
Cálculo da razão de ganho
$$ \text{Gain ratio}(S, A) = \dfrac{G(S, A)}{E(S, A)}$$Índice de Gini
O índice de Gini é outra medida de impureza utilizada para avaliar a heterogeneidade dos dados em relação à classe ou variável de saída.
Mede a probabilidade de dois exemplos escolhidos aleatoriamente pertencerem a diferentes classes.
Cálculo do índice de Gini
$$ \text{Gini}(S) = 1 - \sum_{i=1}^c p_i^2$$em que `\(p_i\)` é a proporção de exemplos na classe `\(i\)` da amostra de treinamento S.
O índice de Gini varia de 0 a 1, sendo 0 quando todos os exemplos pertencem à mesma classe (alta pureza) e 1 quando os exemplos estão igualmente distribuídos entre as classes (alta impureza).
Exemplo
Compra de um computador
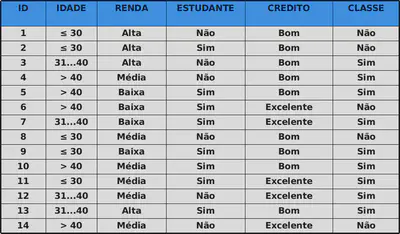
Cálculo da entropia
$$ \text{E(S)} = -\dfrac{9}{14}\log_2 (\dfrac{9}{14}) - \dfrac{5}{14}\log_2 (\dfrac{5}{14}) = 0,940$$
Ganho de informação para o atributo idade
$$ \text{E(S, Idade)} = \dfrac{|\leq 30|}{|S|}\times \text{E}(\leq 30)\\ + \dfrac{|31...40|}{|S|}\times \text{E}(31...40) \\ + \dfrac{|>40|}{|S|}\times \text{E}(>40)$$`
| Classe | ||||
|---|---|---|---|---|
| Sim | Não | |||
| Idade |
=< 30 | 2 | 3 | 5 |
| 31...40 | 4 | 0 | 4 | |
| >40 | 3 | 2 | 5 | |
| 14 | ||||
$$ \text{E(S, Idade)} = \dfrac{5}{|14|}\times \text{E}(\leq 30)+ \dfrac{4}{|14|}\times \text{E}(31...40) \\ + \dfrac{5}{14}\times \text{E}(>40)$$
| Classe | ||||
|---|---|---|---|---|
| Sim | Não | |||
| Idade |
=< 30 | 2 | 3 | 5 |
| 31...40 | 4 | 0 | 4 | |
| >40 | 3 | 2 | 5 | |
| 14 | ||||
$$ \text{E}(\leq 30) = -\dfrac{2}{5}\log_2 (\dfrac{2}{5}) - \dfrac{3}{5}\log_2 (\dfrac{3}{5}) = 0,971$$
$$ \text{E}(31...40) = 0\,\,\,\,\,\,\,\, \text{e} \,\,\,\,\,\,\,\, \text{E}(>40) = 0,971$$
$$ \text{G}(S, \text{Idade}) = \text{E}(S) - \text{E}(S,\text{Idade})\\ = 0,940 - 0,693 = 0,247$$

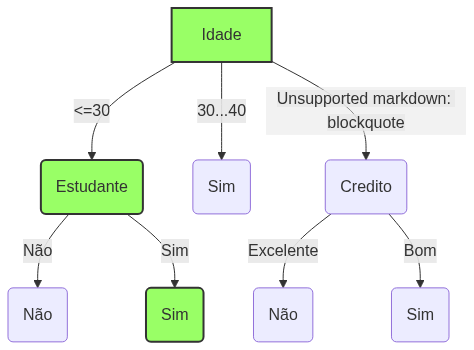
Escolhemos o atributo com maior ganho de informação como nó de decisão. No nosso caso, o atributo Idade. A partir daí, dividimos o conjunto de dados a partir das categorias da variável idade e repetimos o mesmo processo em todos os ramos.
Um ramo com entropia de 0 é um nó folha. Um ramo com entropia maior que 0 precisa de mais divisão.
Árvore estimada
João possui as seguintes características
- menos de 30 anos
- renda média
- é estudante
- possuí um bom crédito na praça!
De volta ao Joãozinho…
João comprará o computador?
De acordo com árvores de decisão: SIM!